CTL*
CTL* is a superset of computational tree logic (CTL) and linear temporal logic (LTL). It freely combines path quantifiers and temporal operators. Like CTL, CTL* is a branching time logic. The formal semantics of CTL* formulae are defined with respect to a given Kripke structure.
Contents |
History
LTL has been proposed for the verification of computer programs first by Amir Pnueli in 1977. Four years later in 1981 E. M. Clarke and E. A. Emerson invented CTL and CTL model checking. CTL* was defined by E. A. Emerson and Joseph Y. Halpern in 1986.
Interestingly, CTL and LTL have been developed independently before CTL*. Both sublogics have become very important in the model checking community, while CTL* is not yet of practical importance. This is surprising because the computational complexity of model checking in CTL* is not worse than that of LTL: they both lie in PSPACE.
Syntax
The language of well-formed CTL* formulae is generated by the following unambiguous (wrt bracketing) context-free grammar:
where  ranges over a set of atomic formulas. Valid CTL*-formulae are built using the nonterminal
ranges over a set of atomic formulas. Valid CTL*-formulae are built using the nonterminal 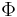 . These formulae are called state formulae, while those created by the symbol
. These formulae are called state formulae, while those created by the symbol  are called path formulae. (The above grammar contains some redundancies; for example
are called path formulae. (The above grammar contains some redundancies; for example 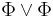 as well as implication and equivalence can be defined as just for Boolean algebras (or propositional logic) from negation and conjunction, and the temporal operators X and U are sufficient to define the other two.)
as well as implication and equivalence can be defined as just for Boolean algebras (or propositional logic) from negation and conjunction, and the temporal operators X and U are sufficient to define the other two.)
The operators basically are the same as in CTL. However, in CTL, every temporal operator (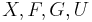 ) has to be directly preceded by a quantifier, while in CTL* this is not required. The universal path quantifier may defined in CTL* in the same way as for classical predicate calculus
) has to be directly preceded by a quantifier, while in CTL* this is not required. The universal path quantifier may defined in CTL* in the same way as for classical predicate calculus 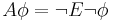 , although this in not possible in the CTL fragment.
, although this in not possible in the CTL fragment.
Examples of formulae
- CTL* formula that is neither in LTL or in CTL:
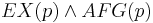
- LTL formula that is not in CTL:
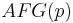
- CTL formula that is not in LTL:
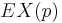
- CTL* formula that is in CTL and LTL:
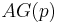
Remark: When taking LTL as subset of CTL*, any LTL formula is implicitly prefixed with the universal path quantifier 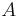
Semantics
The semantics of CTL* are define with respect to some Kripke structure. As the names imply, state formulae are interpreted with respect to the states of this structure, while path formulae are interpreted over paths on it.
State formulae
If a state  of the Kripke structure satisfies a state formula
of the Kripke structure satisfies a state formula 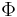 it is denoted
it is denoted 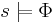 . This relation is defined inductively as follows:
. This relation is defined inductively as follows:
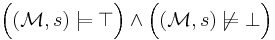
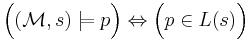
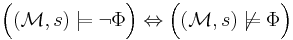
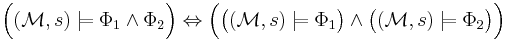
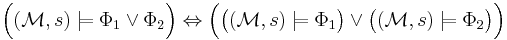
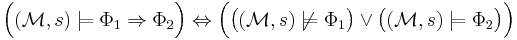
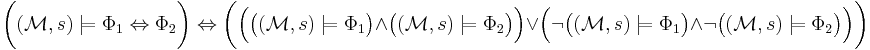
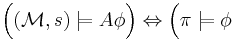 for all paths
for all paths 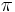 starting in
starting in 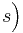
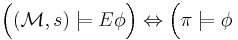 for some path
for some path 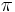 starting in
starting in 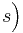
Path formulae
The satisfaction relation 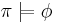 for path formulae
for path formulae 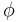 and a path
and a path 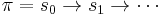 is also defined inductively. For this, let
is also defined inductively. For this, let ![\ \pi[n]](/2012-wikipedia_en_all_nopic_01_2012/I/65938baff175028e9c6f43cf56c5c282.png) denote the sub-path
denote the sub-path 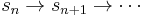 :
:
See also
References
- Amir Pnueli: The temporal logic of programs. Proceedings of the 18th Annual Symposium on Foundations of Computer Science (FOCS), 1977, 46–57. DOI= 10.1109/SFCS.1977.32
- E. Allen Emerson, Joseph Y. Halpern: "Sometimes" and "not never" revisited: on branching versus linear time temporal logic. J. ACM 33, 1 (Jan. 1986), 151–178. DOI= http://doi.acm.org/10.1145/4904.4999
- Ph. Schnoebelen: The Complexity of Temporal Logic Model Checking. Advances in Modal Logic 2002: 393–436
External links
- CTL Teaching slides of professor Alessandro Artale at the Free University of Bozen-Bolzano
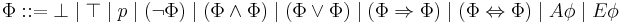
![\phi::=\Phi \mid (\neg\phi) \mid (\phi\and\phi) \mid (\phi\or\phi) \mid
(\phi\Rightarrow\phi) \mid (\phi\Leftrightarrow\phi) \mid X\phi \mid F\phi \mid G\phi \mid [\phi U \phi]](/2012-wikipedia_en_all_nopic_01_2012/I/7d2b54a640e7e1ff1640d1742c490330.png)
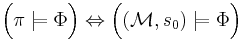
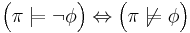
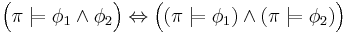
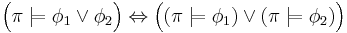
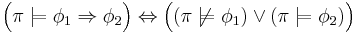
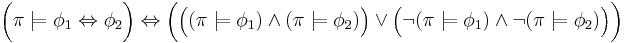
![\Big( \pi \models X\phi \Big) \Leftrightarrow \Big( \pi[1] \models \phi \Big)](/2012-wikipedia_en_all_nopic_01_2012/I/71f22eb326e8762f3235ec0f28eefbf7.png)
![\Big( \pi \models F\phi \Big) \Leftrightarrow \Big( \exists n\geqslant 0: \pi[n] \models \phi \Big)](/2012-wikipedia_en_all_nopic_01_2012/I/af2c03b27ebd921c72bb99ca6876b4b3.png)
![\Big( \pi \models G\phi \Big) \Leftrightarrow \Big( \forall n\geqslant 0: \pi[n] \models \phi \Big)](/2012-wikipedia_en_all_nopic_01_2012/I/db6a918d36c7e3a20ad3456a8cb73fcb.png)
![\Big( \pi \models [\phi_1U\phi_2] \Big) \Leftrightarrow \Big( \exists n\geqslant 0: \big(\pi[n] \models \phi_2 \land \forall 0\leqslant k < n:~ \pi[k] \models \phi_1 \big)\Big)](/2012-wikipedia_en_all_nopic_01_2012/I/9e4129d5c0c10c801fc70eac124fd940.png)